入試分析/解答速報
2024年02月01日

看護医療系専門進学塾の桜芽会です。
桜芽会では、各大学の看護系学科について、入試問題の解答解説を載せていきます。
今回は、2024年度 東京家政大学 統一地区 2日目(数学)の解答解説を載せます。
東京家政大学を志望している生徒は是非参考にしてください!
【講評】
1日目と同じく数Ⅰ、数Aからの出題であるため、こちらも範囲としては広くはない。
1日目と異なる点は、問題数が多いことである。1日目が大問2問であるのに対し、2日目は大問4問構成となっている。
難易度は1日目とさほど変わらない印象。また、「え、それ聞いてくるのか・・・」という変化球的な問題や、(私個人として)意図の分からない解答欄がチラホラ見られるのも1日目と同様である。
ただ、1日目の講評でも書いた通り、出題範囲が少ないということは、スタンダードな問題だけでは点数が開きにくいのだろうと思う。
ミスなどを除けば、変化球で聞いてくる問題が合否の分かれ道になっているのではないだろうか。
大問1は小問集合。数Ⅰ、数Aの範囲から満遍なく出題されている。難易度としては1日目の小問集合とさほど変わらない印象。
スタンダードな問題と、変化球の問題が混在しており、連番問題もないので、試験時間を考えながら効率的に解ける問題から優先的に手をつけて欲しい。
スタンダードな問題の中にもやや計算が面倒な問題があるので、いかに早く、正確に計算できるかが重要である。
大問2は二次関数の問題。これは共通テストを意識したような、現実の世界に数学を応用している長文問題である。
難易度としては大問4問の中で最も優しいので、落ち着いて文章を正確に読み取れば得点源になったはずだ。
大問3はデータ分析の問題。典型問題から、ちょっと選択肢で「アレ?」となってしまう問題までがあるが、箱ひげ図や相関係数などの定義がしっかりと理解できていなければ得点ができなかったと思う。
大問4は平面図形の問題。これは重心、内心、外心、垂心などの基本が問われてている。
ただし、定義だけを丸暗記していても解ける問題ではなく、中学範囲の相似を始め、実際に図形を自分で書いてみるといったような作業ができない受験生は苦戦したのではないだろうか。
解答
| Ⅰ | 解答 | Ⅱ | 解答 | Ⅲ | 解答 | Ⅳ | 解答 |
|---|---|---|---|---|---|---|---|
| 1 | 4 | 23 | 5 | 43 | 3 | 48 | 3 |
| 2 | 6 | 24 | 2 | 44 | 0 | 49 | 2 |
| 3 | 2 | 25 | 0 | 45 | 8 | 50 | 2 |
| 4 | 1 | 26 | 2 | 46 | 7 | 51 | 9 |
| 5 | 2 | 27 | 2 | 47 | 3 | 52 | 0 |
| 6 | 1 | 28 | 0 | 53 | 4 | ||
| 7 | 2 | 29 | 2 | 54 | 9 | ||
| 8 | 2 | 30 | 2 | 55 | 0 | ||
| 9 | 4 | 31 | 0 | 56 | 6 | ||
| 10 | 1 | 32 | 1 | 57 | 0 | ||
| 11 | 7 | 33 | 2 | 58 | 3 | ||
| 12 | 1 | 34 | 5 | ||||
| 13 | 5 | 35 | 5 | ||||
| 14 | 4 | 36 | 4 | ||||
| 15 | 3 | 37 | 3 | ||||
| 16 | 2 | 38 | 0 | ||||
| 17 | 1 | 39 | 6 | ||||
| 18 | 0 | 40 | 4 | ||||
| 19 | 9 | 41 | 3 | ||||
| 20 | 6 | 42 | 2 | ||||
| 21 | 4 | ||||||
| 22 | 0 |
解説
※アプローチを解説するだけですので、計算などの詳細が知りたい方はぜひ桜芽会をご利用ください。
Ⅰ
(1)
絶対値不等式の問題。左辺全体の不等式は-3から3で挟むことで取ることができる。
ここで-2を取るために全てのへんに2を足すわけだが、そうすると、
-1≦|x-1|≦5が得られる。絶対値は必ず0以上なので、これを0≦|x-1|≦5と修正していないと混乱してしまう。
あとは通常の絶対値不等式と同じように-5と5で挟んで絶対値を取れば良い。
(2)
通常の因数分解。これは問題集でも何度か演習したことがあるはずである。xの降べき順に項を並び替え、x2、x、x0で各項を括ってたすき掛けを行えば良い。
穴埋め箇所にヒントがあるので、それをいかに活用するかで計算スピードに差が出た問題ではないだろうか。
(3)
集合の問題。ベン図を書いて各要素を入れていけば自ずと正解が導かれる。
後の平面図形の問題でもそうだが、ベン図をはじめグラフや図形など、自らの手で書きながら問題を解く癖をつけて欲しい。
(4)
二次関数の並行移動、対称移動に関する問題。並行移動の公式、対称移動の公式を覚えていないと、頂点や軸から算出することになる。
x方向にp、y方向にq並行移動:元の式のxに(x-p)を、yに(y-q)を代入する。
x軸に関して対称移動:yに-yを代入する。
y軸に関して対称移動:xに-xを代入する。
(参考①)原点に関して対称移動:xに-x、yに-yを代入する。
(参考②)y=xに関して対称移動:xとyを入れ替える。
ただ、公式を覚えていても移動が多いので計算ミスが多発した問題かもしれない。
(5)
三角比と平面図形の問題。「円に内接する四角形は対角線を引くことにより二つの三角形に分け、円に内接する四角形の対角の和が180°になることを利用して余弦定理を使う」という典型問題。
cosの値を求めたのち、sinに変換し、sinを用いた三角形の面積公式を用いて2つの三角形の面積を求め、合計すれば良い。
典型パターンの補助線、余弦定理、sinを用いた三角形の面積公式に加え、三角比の角度変換(sin(180°-θ)=sinθ、cos(180°-θ)=-cosθなど)が分かっていないと解けない問題。
(6)
データ分析の問題。分散の定義式が分かっていても、その意味を理解していないととんでもなく時間がかかる問題。
もちろん、この問題では実際に分散を計算してはいけない。分散とはデータの散らばりを表す問題なので、まずは平均値を算出する。
5点を加えることにより、平均値に近づくことになれば分散は小さくなり、逆に5点を加えることにより平均値から遠ざかることになれば分散は大きくなる。
平均値は44なので、40点以下の人に5点を加えると、44点に近づいてしまう。
(7)
順列の問題。これは典型的な並べ替えの問題なので、問題集が定着していればサービス問題である。
逆に解法を知らなければ、Xが1番左にある時から順に並べ方を数えていく必要があるのでとんでもなく時間がかかる。
XとYを同じ文字として扱い、同じものを含む順列として解くことができていれば良い。
(8)
不定方程式の問題。問題集では「この式の一般解を求めよ」という形で見たことがあるかと思う。
まずは不定方程式を解き、一般解を算出した上で、x+yを計算すると、-5k+1となる。
この中で1番100に近い数字を見つけると、k=-19のとき、x+y=96となる。
一般解を求めるところまでは問題集でやったことがあっても、一捻りを入れられたことで解けなかった受験生もいるかもしれない。
(9)
平面図形の問題。高校範囲ではなく、中学範囲の平面図形の問題である。
接弦定理と円周角(直径の円周角は90°)、円に内接する四角形の対角の和が180°を使えばxが求められる。
看護受験でありがちなのがこの中学範囲の問題である。受験を焦るあまり、中学数学がおざなりになった状態で高校範囲を演習していても、このような問題に足をすくわれるので注意。
Ⅱ
二次関数の文章問題。共通テストを意識(?)している感じの長文問題である。
二次関数の基礎がしっかりできていることはもちろん、正しく、正確に問題文を読み取る能力が必要だ。
まずはtとyの値が2組与えられていること、条件からこの関数は原点を通ることが分かっているので、一般式をy=ax2+bxとおき、t=1,y=15とt=2,y=20を代入してa,bを求める。
最高点を求めるには、この関数の頂点を求めれば良いので平方完成を行う。
さて、次にシャッターのタイミングなのだが・・・。シャッターのタイミングがt=〇〇の場合が聞かれているが、これは空欄26と同じなので空欄29の意味があまりよく分からない。
とにかく、あとはt=2を代入してt=2-0.2などを計算し、元の式に代入することで最高到達点からの差も求めることができる(差が文字になっていても問題ない。そのまま元の式のtに代入するだけ)。
この差を5センチ以内にする問題も、(32、33、34で求めた式)≦5を解くだけだ。
区間の秒数については、問題で与えられた不等式を解くだけ。
最後の問題は問題文に惑わされないように注意しよう。問題文ではまず「最高点までの距離を求める」ことが記されているが、前半部分で行うのはあくまでもボールを打ってから落下するまでの距離から、ボールの飛距離に関する一般式を作ることだ。
ここでx方向の距離がtによって表される。
あとは最高点までの距離を斜辺と見立てて、x方向の距離はt=2を代入して60、最高到達点は20なのでこの2つの情報から三平方の定理で斜辺(最高到達点までの距離)を求めれば良い。
最後は先ほど求めた距離を最高到達点までにかかる時間(t=2)で割って終了。
Ⅲ
(1)
箱ひげ図に関する問題。第一四分位数は6番目と7番目の平均(37.5)、中央値は13番目(54)、第三四分位数は19番目と20番目の平均(65)。
(2)
③がすごく不気味な問題。ただ、そこまで深読みせずにここは⓪を選べば良い。次の(3)でも相関係数が0.87なので合わせて問題ないかと思われる。
(3)
平均点はダミー。標準偏差と共分散から公式によって求められる。公式を知っている人からすればサービス問題。
(4)
良い問題。これを疎かにしている受験生は多かったのではないだろうか。良問なので詳しい解説はこちらをご参照いただきたい。
Ⅳ
(1)(2)(3)
Ⅳは全体的に中学範囲の問題(高校でも学ぶが)。重心、内心、外心、垂心の定義と相似がうまく見つけられるかがポイント。
外心の問題のみ、普通に求めると答えにたどりつかない(他の方法だとスムーズなのか?)。
普通に求めると選択肢の答えに辿りつかないので、三平方の定理を用いて選択肢の文字に合うように答えを変換する必要がある。
ちなみに絶対値がついているのは、鋭角三角形ならばb>aだが、鈍角三角形だとb<aとなるためである。
※すみません、最後の画像、落書きが消せませんでした・・・・緑と青の三角形の相似で解きます。
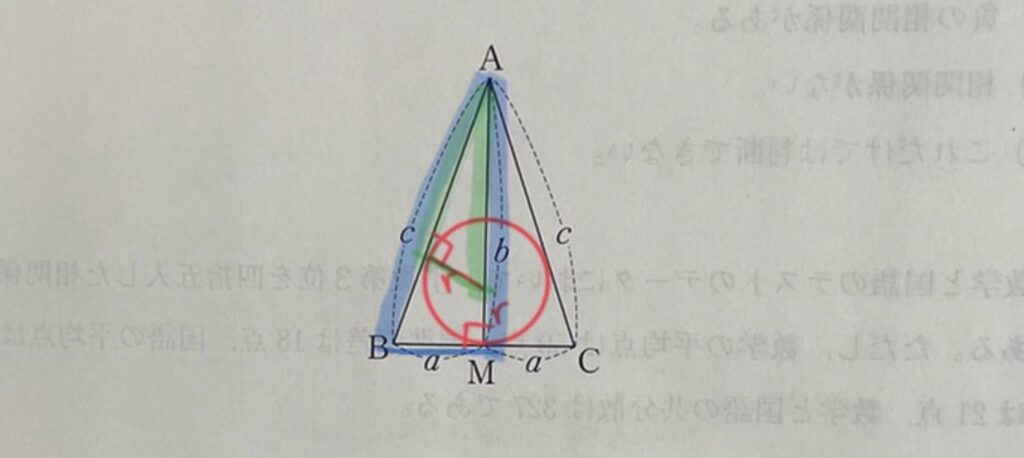
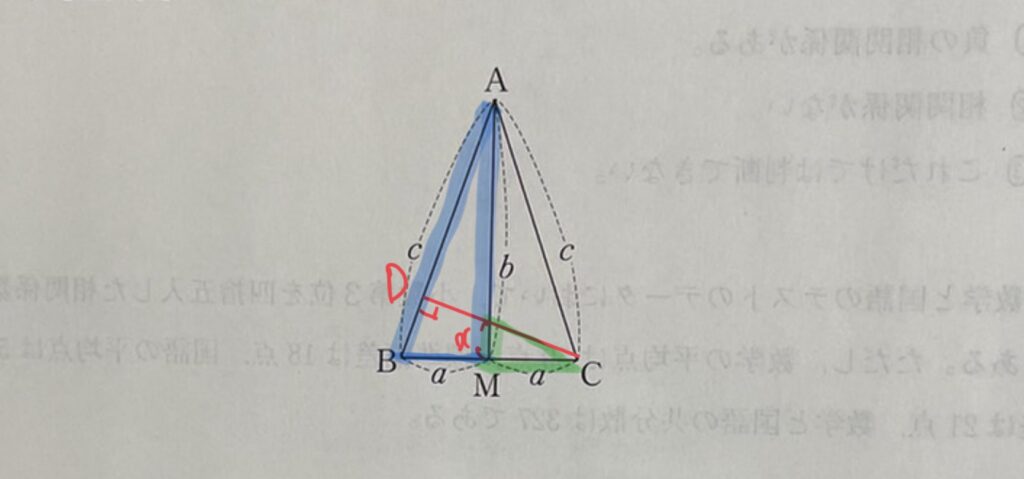
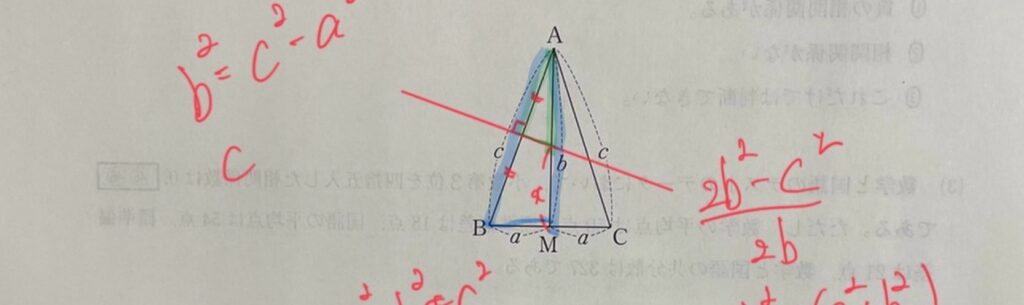
また、角度の問題に関しては自分で鋭角三角形、直角三角形、鈍角三角形を書いて見れば明らかなのだが、図形を自分で書かない受験生は苦労した問題だろう。
(4)
垂心と重心が一致するのは正三角形。これも他のパターンがあるので、ぜひこちらのサイトを参考にしてもらいたい。
GM、HM、OMの長さはすでに前までの問題で求めてあるので、OGとOHの長さを求めれば終了。
看護医療系専門進学塾桜芽会の講習
2024年度春期講習の概要はこちら
オンライン
進学セミナー募集開始

無料LINE相談
随時受付中
無料
体験・相談
お申し込み


 アクセス
アクセス
