看護医療系専門進学塾の桜芽会です。

桜芽会では、各大学の看護系学科について、入試問題の解答解説を載せていきます。

今回は、2024年度 杏林大学 保健学部 学校推薦型選抜入学試験 適性検査 数学の解答解説を載せます。

杏林大学 保健学部を志望している生徒は是非参考にしてください！

【講評】

出題範囲から満遍なく出題されており、レベルとしては学校の問題集レベルである。多くの問題集やレベルの高い問題集に手を出すのではなく、学校で配られるレベルの問題集を1冊完璧に仕上げれば問題なく90点以上を目指せる。

気になる点としては、一部中学数学からの出題が見られることが挙げられる。例えば問44や問45の有理数と無理数の単元の問題は、中学3年生で習う範囲であり、油断しているとやり方を忘れてしまっている・・・ということになりかねないので注意が必要である。

また、これは他の大学の入試においても重要なことであるが、記述式でなくマーク式の場合は、まっすぐ問題を解くよりも選択肢を利用して解いた方が簡単な場合もある。

マーク式の問題の解き方に慣れるためにも過去問は重要である。

問題に関しては、杏林大学HPにアップされているので確認すること。

その他の科目、大学の過去問解答/解説はこちら。

【解答解説】

問41.
100の正の約数の総和を求めるためには、まず100の素因数分解を行う

100は2と5の2乗で表される。つまり、100 = 2² × 5²である。

正の約数の総和を求める公式は次の通り。

N=p^a×q^b×r^cと素因数分解される時

約数の総和＝(p⁰+p¹+p²+…+p^a)×(q⁰+q¹+q²+…+q^b)×(r⁰+r¹+r²+…+r^c)

この公式を用いて、100の正の約数の総和を求める：

(2⁰+2¹+2²)×(5⁰+5¹+5²)=(1+2+4)×(1+5+25)=7×31=217

したがって、100の正の約数の総和は217。

問42.
4で割って3余る数は\(4m+3\)、4で割って4余る数は\(7n+4\)（m、nは整数）と表すことができる。

今求めたい数はこの両方で表されるはずなので、\(4m+3=7n+4\)（①）。

m=2、n=1はこの式の解の一つなので、①に代入して\(4×2+3=7×1+4\)（②）

①-②より\(4(m-2)=7(n-1)\)

4と7は互いに素なので、\(m-2=7p\)、\(n-1=4q\)（p、qは整数）と表せる。

\(n-1=4q（n=4q+1）\)を\(7n+4\)に代入すると、\(28q＋11\)となり、qの値を変化させて3桁の整数で1番小さいものを探せば良い。

\(q=4\)のとき123となるため、求める値は123である。

補足：上記のように求めるのが正しい解法であるが、本問題はあらかじめ5つの選択肢が与えられている。一つずつ4と7でそれぞれ割ってみて余りが題意の通りになる数を探しても良い。

問43.
7進法で表すと2桁になる自然数は、7進法での10から7進法の最大の2桁の数である66までの数である。

7進法を10進法に変換するためには、各桁の値をその桁の基数（7のべき乗）で掛けて足し合わせる。具体的には次のとおり：

1 × 7¹ + 0 × 7 ⁰= 7 + 0 = 7（10進法）

6 × 7¹ + 6 × 7⁰ = 42 + 6 = 48（10進法）

したがって、7進法で2桁になる自然数は、10進法で7から48までの42個。

問44.
循環小数0.261（循環部分は261）を分数に変換する手順は次のとおり。

まず、循環小数を表すための変数を設定する。この場合、\(x=0.261261261… x=0.261261261…\)。

次に、10の3乗（つまり1000）を掛けて、循環部分を整数にする。これにより、

\(1000x=261.261261…\)
\(x=0.261261261……\)となる。

これらの2つの式を引き算すると、\(1000x−x=261\)。これを整理すると、\(999x=261\)となる。

最後に、両辺を999で割ると、\(x=\)\(\displaystyle\frac{261}{999}\)となる。

したがって、循環小数0.261（循環部分は261）を分数にすると、\(\displaystyle\frac{261}{999}\)。この分数はさらに約分でき、最終的に\(\displaystyle\frac{29}{111}\)となる。

問45.
まず\(2\)\(\sqrt6 \)の整数部分を求める。\(2\)\(\sqrt6 \)を2乗すると24。

\(4^2<24<5^2\)であるから、\(2\)\(\sqrt6 \)の整数部分は4。

少数部分は\(2\)\(\sqrt6 \)から整数部分の4を引けば良いので、

\(a=2\)\(\sqrt6 \)\(-4\)

これを題意の式に代入すると

\((2\)\(\sqrt6 \)\(-4)^2+8(2\)\(\sqrt6 \)\(-4)-5=3\)

よって答えは3となる。

問46.
二次関数の最小値、最大値は平方完成を行い、グラフを作成して求める。

\(y=−2x^{2}+8x+1({定義域-1≦x≦3}）\)を平方完成すると、\(y=−2(x-2)^{2}+9\)となり、グラフは図のようになる。

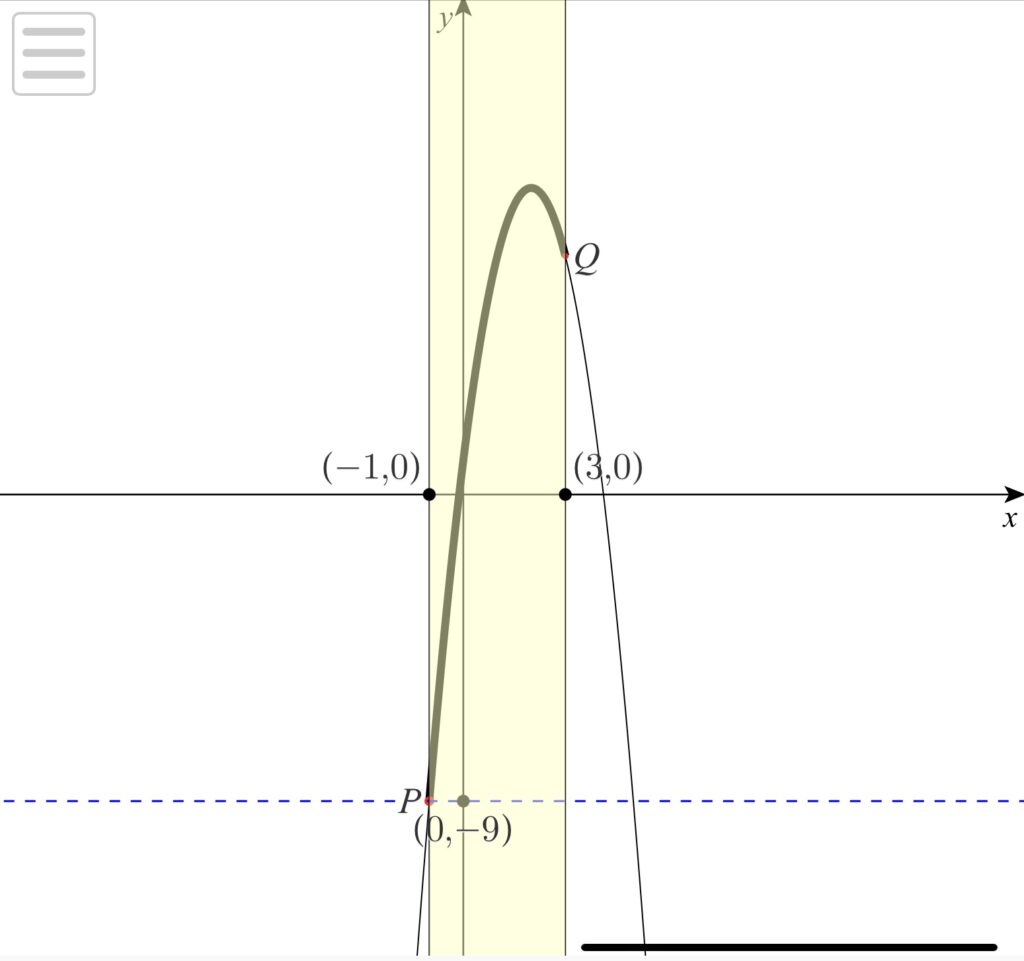
よって、x=-1のとき最小値y=-9となる。

※最大値はx=2のときy=9

問47.
\(y=x^{2}+2kx−3k＋4\)とすると、すべての実数xについて\(y>0\)であれば良い。

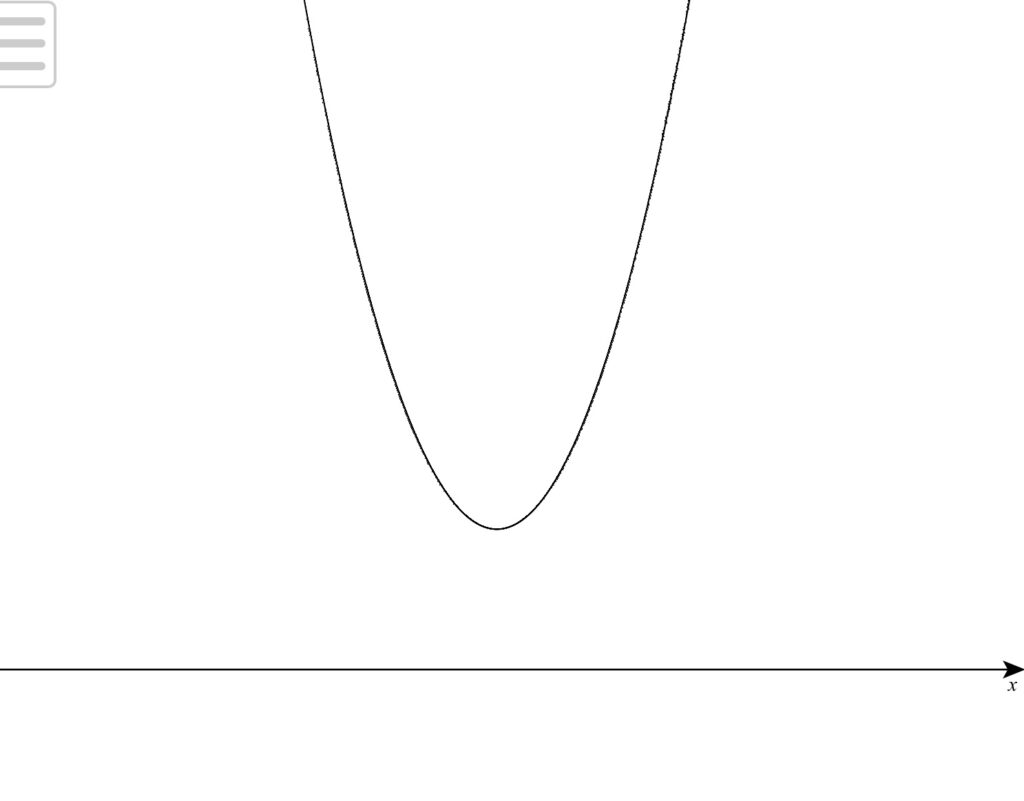
つまり、\(y=x^{2}+2kx−3k＋4\)のグラフが右図のように常にx軸よりも上部（接してしまうと\(y≧0\)となってしまうので不適）に位置しなければならない（※）。

ここで、\(x^{2}+2kx−3k＋4=0\)の判別式を\(D\)とすると、※を満たす条件は\(D<0\)である。

\(D/4=k^2-(-3k+4)=(k+4)(k-1)\) \(D<0のとき\)

\((k+4)(k-1)<0\) よって\(-4<k<1\) となる。

補足：判別式と二次方程式の実数解、二次関数とx軸の位置関係について理解していない人は必ず問題集で復習してほしい。また、二次不等式の計算も復習しておくこと。

問48.
まずは2辺の長さと1つの角度が分かっているので、余弦定理によってBCの長さを求める。

\(BC^2=AB^2+AC^2-2AB×AC×cos120\)

\(BC^2=5^2+3^2-2×5×3×\)\(\displaystyle\frac{-1}{2}\)

これを計算すると、\(BC=7\)

また、角のニ等分線定理より、\(AB:AC=AD:CD=5:3\)

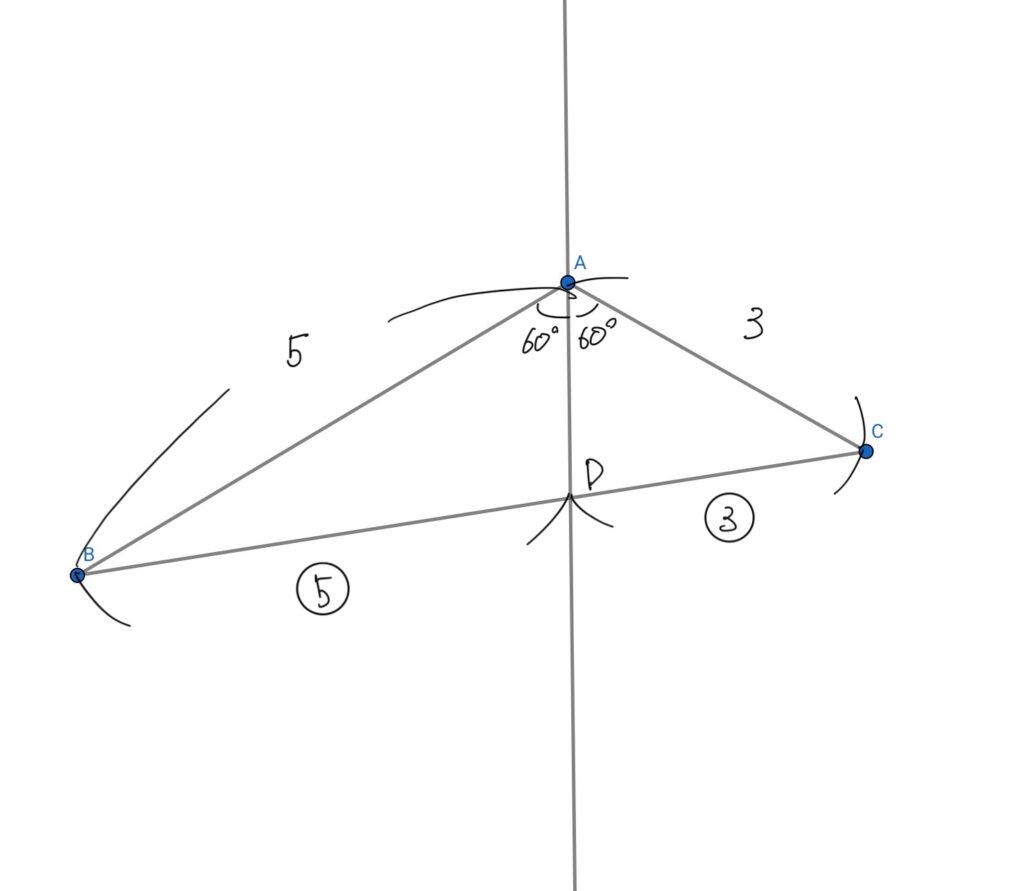
よって、\(BD=7×5/8=\)\(\displaystyle\frac{35}{8}\)

補足：正弦定理や余弦定理を使うことはすぐに思いつく人が多いだろうが、角の二等分線定理は意外と忘れがち。角の二等分線があったら90%くらい角の二等分線定理を使う！ということを常に意識しておくこと。

49.
3辺の長さが分かっているのでまずは余弦定理によりどれか1つの角の\(cos\)の値を求める。（以下では\(cosA\)の値を求める）

\(3^2=6^2+5^2-2×5×6×cosA\)

これを解くと\(cosA=\)\(\displaystyle\frac{13}{15}\)

これを\(sin^2θ+cos^2θ=1\)に代入して解くと

\(sinA=\)\(\displaystyle\frac{2\sqrt{14}}{15}\) (\(0<A<180\))

これを三角形の面積公式に代入して\(△ABC=\)\(\displaystyle\frac{1}{2}\)\(×6×5×\)\(\displaystyle\frac{2\sqrt{14}}{15}\) \(=\)\(2\sqrt{14}\)

問50.
まずは一般的な解き方を示したのち、マーク式（途中式なし）テストの場合の解き方を示す。

空間図形は求めたい長さや角度が含まれる平面に注目することが重要である。

一般的な解法の場合、平面ABEでの切り口を考える。AE、BEはそれぞれ正三角形の頂点を含む底辺の垂直二等分線なので、30°、60°、90°直角三角形の辺の比（\(1：2：\)\(\sqrt3 \))を利用してAE=BE=\(3\sqrt3 \)

ここで \(BH=x\)とおくと、各辺の長さは以下の通りとなる。

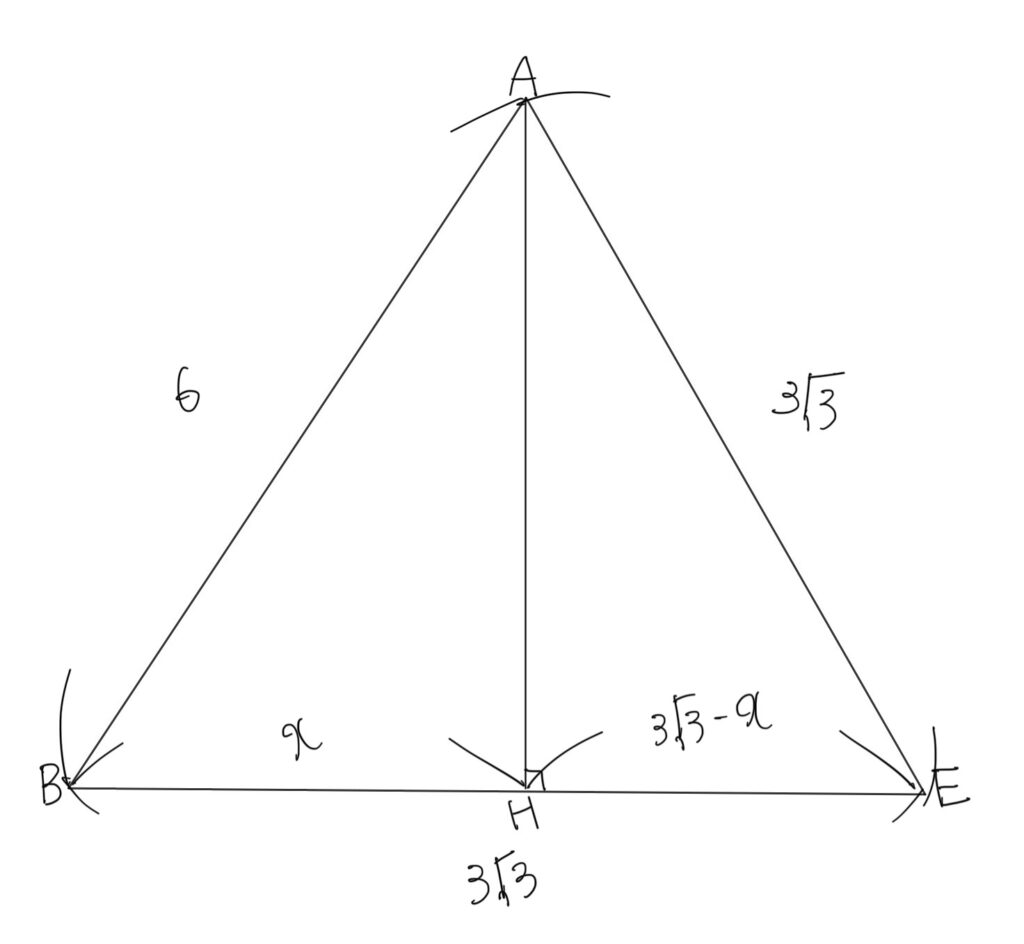
\(△ABHと△AEHのAH\)の長さについてそれぞれ三平方の定理を利用すると

\(AH^2=6^2-x^2\)

\(AH^2=(\)\(3\sqrt3 \) \()^2-(\)\(3\sqrt3 \) \(-x)^2\)

これを連立して、 \(6^2-x^2=(\)\(3\sqrt3 \) \()^2-(\)\(3\sqrt3 \) \(-x)^2\)

よって、 \(x=\)\(2\sqrt3 \)

\(AH^2=6^2-(\)\(2\sqrt3 \) \()^2=24\)

\(AH=\)\(2\sqrt6 \) \((x>0)\)

通常はこのような流れで解くが、本問は記述式ではなくマーク式である。正四面体の頂点から底面に下ろした垂線の足は底面の正三角形の重心と一致することを知っていれば、以下のように解くことができる。

※感覚的に垂線の足と正三角形の重心が一致することは明白だが、記述式の場合はこれを証明する必要がある。

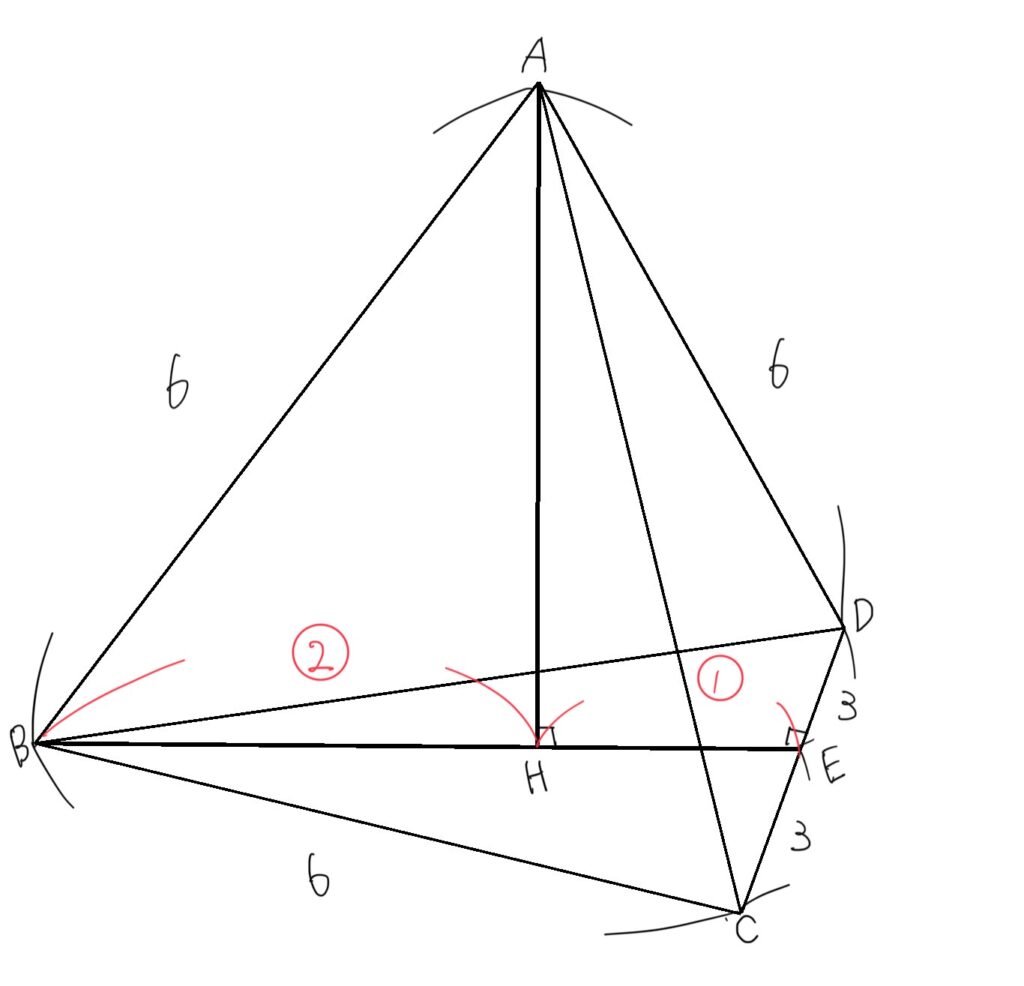
三角形の重心は各中線を \(2:1\)に内分するため、\(BE=\)\(3\sqrt3 \) より\(BH=\)\(2\sqrt3 \) 、\(EH=\)\(\sqrt3 \)を求め、\(△ABHまたは△AEH\)で三平方の定理を用いて\(AH\)の長さを求めても良い。

問51.
グループ（この場合は部屋）に区別がある場合は、どのグループに所属しているかを区別する必要がある。

\({}_6 C_2\) ×\({}_4 C_2\) ×\({}_2 C_2\) =90

よって90通り。

補足：もしグループが2人、2人、2人で部屋の区別がない場合は、グループの区別をしなくても良いので3つのグループの並び替え順（\(3!\))で割ると良い。

問52.
1から5までの数字が書かれた5枚のカードから順番にカードを取り出す場合の数は、1回目は5枚から1枚を選び、2回目は残りの4枚から1枚を選ぶと考えると5×4=20通り。

Xの値が1になるのは

1回目・・・5 2回目・・・4
1回目・・・4 2回目・・・3
1回目・・・3 2回目・・・2
1回目・・・2 2回目・・・1
の4通り。

よって、4÷20=0.2

問53.
標準偏差はデータの散らばり具合を表す。元のデータに定数を加算した際は変化なし、定数倍したときはその定数倍されるという性質を持つ。

よって、20× 2＝20

補足①：例えば5と7というデータの散らばり具合について考えたとき、平均は6である。2倍すると10と14となり平均は12。元のデータの散らばり具合が平均に対して1と-1であるのに対して、2倍したデータの平均からの散らばり具合は2と-2で2倍になっている。

補足②：一方、5と7という元のデータから3を引くという行為を考えてみると、3を引いた後のデータは2と4となり平均は3。データの散らばり具合は1と-1で、元のデータの散らばりと変わらないことがわかる。

補足③：元データを操作した際の平均値、分散、標準偏差の変化について覚えられていない場合は要復習。

問54.
分散の定義に沿って方程式を作る。

σ^2=(二乗の平均)-(平均)^2

二乗の平均はaを用いて\(\displaystyle\frac{1^2+4^2+a^2}{3}\)\(=\)\(\displaystyle\frac{17+a^2}{3}\)と表せる。

一方、平均の二乗は\((\displaystyle\frac{1+4+a}{3})^2\)\(=\)\((\displaystyle\frac{5+a}{3})^2\)と表せる。

よって上記の公式に代入して

\(6=\)\(\displaystyle\frac{17+a^2}{3}\)\(–\)\((\displaystyle\frac{5+a}{3})^2\)

この方程式を解くと、\(a=7、-2\)

\(a>0\)なので、\(a=7\)

平均の二乗の式に代入すると、平均の二乗は16、よって平均は4となる。

問55.
条件付き確率の公式より

\(P_B(A)=\displaystyle\frac{P(A\cap B)}{P(B)}\)。よって\(P(A\cap B)\)と\(P(B)\)の値を求めれば良い。

条件より\(P_A(B)=\displaystyle\frac{P(A\cap B)}{P(A)}=0.9、P(A)=0.1\)なので、代入して解いて

\(P(A\cap B)=0.9×0.1=0.09\)

また、\(P_\bar{A}(B)=\displaystyle\frac{P(\bar{A}\cap B)}{P(\bar{A})}=0.3\)、\(P(\bar{A})=1-P(A)=0.9\)なので、代入して解いて

\(P(\bar{A}\cap B)=0.3×0.9=0.27\)

また、\(P(B)-P(A\cap B)=P(\bar{A}\cap B)\)なので、これを解いて

\(P(B)=0.36\)

よって、\(P_B(A)=\displaystyle\frac{P(A\cap B)}{P(B)}=0.09÷0.36=0.25\)

補足：本問は事象Aと事象Bの独立性が問題文に記述されておらず、一瞬ドキッとするが、結果的に従属。
（独立ならば\(P(A\cap B)=P(A)×P(B)\)が成り立つので一瞬で結果が求まってしまう。答えを見ても\(P(B)≠P_\bar{A}(B)\)なので事象Aと事象Bは従属）

看護医療系専門進学塾桜芽会の講習

2023年度直前講習の概要はこちら

2024年度春季講習の概要はこちら

その他入塾やご質問事項に関しては、「お問い合わせ」または「LINE無料相談」からお気軽にご連絡ください。