入試分析/解答速報
2024年01月30日

看護医療系専門進学塾の桜芽会です。
桜芽会では、各大学の看護系学科について、入試問題の解答解説を載せていきます。
今回は、2024年度 東京家政大学 統一地区 1日目(数学)の解答解説を載せます。
東京家政大学を志望している生徒は是非参考にしてください!
【講評】
出題範囲は数Ⅰ、数Aのみなので、範囲としては多くはない。問題数も大問2問と少なく、その問題数の中に数Ⅰ、数Aの問題が満遍なく散りばめられている印象。
大問1は小問集合、大問2は三角比と図形の単元になっている。難しい問題、簡単な問題の差が激しいので、難しい問題は思い切って飛ばす勇気が必要だ。
問題自体はそこまでの難問ではないが、細かいところに神経を使う問題が多い印象。
「解き方はなんとなく分かる」「見たことはある」問題ばかりだと思うが、油断していると思わぬところで足をすくわれたり、ミスが発生してしまう。
よって、大問が2問のみという問題数が少ないにも関わらず、細かいところに気を回した結果、時間が足りないと感じた受験生も多いのではないだろうか。
マーク式の試験によくある、問題文中のヒントや誘導が重要な問題もある。
ただし、誘導に乗っかりすぎると解けなくなったり、アプローチが見えなくなるような問題もあるので、この辺りはマーク式の解き方のテクニックや過去問演習で感覚を養ったほうが良いだろう。
教科書傍用に出てくるようなスタンダードなアプローチの問題もあれば、ちょっとマニアック(学校では習っていない人もいるのではなかろうか?)という解法も誘導されているので、塾などで解法をたくさんストックしている受験生に有利だったように思う。
また、連番の問題であっても、前の問題の結果を使わなくても解ける問題もある。
連番問題の前半はその答えを次に使うものと、問題へのアプローチを狭めるものがあるので、後者であれば前半が解けていなくてもアプローチを変えれば解くことができる。
連番問題の前半が解けないからといって諦めず、問題全体を見た上で1点でも多く得点してほしい。
【解答】
| Ⅰ | 解答 | Ⅱ | 解答 |
|---|---|---|---|
| 1 | 2 | 22 | 2 |
| 2 | 2 | 23 | 6 |
| 3 | 2 | 24 | 3 |
| 4 | 3 | 25 | 6 |
| 5 | 3 | 26 | 3 |
| 6 | 2 | 27 | 2 |
| 7 | 1 | 28 | 6 |
| 8 | 2 | 29 | 2 |
| 9 | 0 | 30 | 4 |
| 10 | 3 | 31 | 3 |
| 11 | 2 | 32 | 3 |
| 12 | 0 | 33 | 3 |
| 13 | 1 | ||
| 14 | 2 | ||
| 15 | 5 | ||
| 16 | 6 | ||
| 17 | 4 | ||
| 18 | – | ||
| 19 | 6 | ||
| 20 | 1 | ||
| 21 | 5 |
解説
Ⅰ
(1)
式の計算の問題。絶対値を含む式なので、受験生の対策が薄いところをよく狙ってきている問題。
とりあえずこのままではどうしようもないので、絶対値を含む式を2乗するところから始める。
ここで絶対値の計算問題を疎かにしている受験生は、|x-y|2と(|x|-|y|)2がこんがらがり、(1)からペースを乱されたかもしれない。
落ち着いて考えてみると、|x-y|2と(x-y)2は同じなので、実はこの絶対値は最後の解を選別するところでしか使わない。
※最後の答えで平方根を取る際に、絶対値なので正の方を取れば良い。
対称式と交代式の問題は、教科書傍用レベルの問題集でも頻繁に出題されているので絶対値さえなければ問題なく解ける問題である。
最後に二重根号を外さなければならず、これも基本計算を疎かにしている受験生をふるいにかけるいやらしい問題である。
(2)
因数分解の問題。これは直接計算ではなくマーク式である利点を最大限に活かさなければ、解答は難しい。因数分解後の前半部分(x-y-z)に注目する。
すると、与式の後半部分に3x+3y-3zという項があるので、これを3でくくると(x+y-z)という因数が得られる。
与式の前半部分においても、(x+y-z)を因数として出したいので、x2-2y2-xy+2yz-zxを変形する。
パッとみたところ、-2y2と+2yzが2yでくくれそうだが、これでは(x+y-z)が因数として出てこない。
そこで、x2-2y2-2xy+xy+2yz-zxと変形すると、-2y2-2xy+2yzとx2+xy-zxに分けて共通因数で括れ、無事に(x+y-z)という因数が得られる。
(3)
命題の真偽の問題であるが、これは非常にいやらしい問題。⓪と①のどちらかが間違っているように見えるようにしている意図が見て取れる。
③の反例がx=2であることが明らかなので、もしかするとこれは選択肢に救われた受験生も多いのではないだろうか。
⓪と①は対偶を取ればわかりやすい。
(4)
これは式の形がいかにも因数分解を誘っている。因数分解できることに気づかなければ(解の公式などを使ってしまうと)面倒臭い問題となってしまう。
ちなみに、この因数分解は比較的優しい因数分解であるが、選択肢に不等式の解が与えられているので、これも選択肢に救われた受験生もいるかもしれない。
因数分解後は、解の大きさを判定する必要がある。a2+2と2aの大きさを判定するわけだが、これは不等式の証明で学んだ通り、a2+2-2aを平方完成すれば良い。
(5)
三角比と平面図形の問題。私の授業では「三辺の長さがわかっている三角形はどうにでも料理できる」と教えているので、私の授業を受けたことがある生徒はこの問題を見て少しホッとしたはずだ(笑)。
三辺が分かっている状態で角度を求めるのだから、これはもう余弦定理一択だろう。
さて、後半部分であるが、内接円の半径を求める問題は超典型問題である。△ABCの面積を2通りで表し、方程式を作る。
1通り目はsinを使った三角形の面積公式で求め、2通り目は内接円の半径を高さとして、内接円の中心(Iとする)で△ABCを3つの三角形に分けて△ABC=△IAB+△IBC+△ICAとして面積を求める。
(6)
データの分析の問題。最大値、最小値、四分位数をそれぞれ求めれば消去法で答えが求められる。
最小値は5以上10未満、最大値は35以上40未満(この時点で③は×)、第一四分位数は5個目と6個目のデータの平均なので15以上20未満、中央値は11個目のデータで15以上20未満(この時点で②は×)、第三四分位数は16個目と17個目のデータの平均なので25以上30未満(この時点で①は×)となる。
(7)
場合の数の問題。今回の試験の中で最も得点率が低いと思われる問題の一つ。実はこの問題、誘導がない方が解ける人が多いかもしれない。
というのも、後半部分だけであれば樹形図を書いて数え上げれば十分答えを導き出せるからだ。
前半の誘導に関しては、学校で習っていない人も多いのではないだろうか。この解法についてはこちらのサイトが参考になるので、ぜひ見ておいてほしい。
(8)
有理数と無理数の問題。これも細かいところまで神経を使わなければ、「解けたつもり」になってしまう問題の一つである。
ルートの中身は因数分解が可能で、(n-2)(n+1)となる。
ルートは中身が2乗の数になれば外すことができるが、n-2=n+1とはならないので、可能性があるとすれば、以下のような場合が考えられる。
①(n-2)(n+1)=0となる
②n-2=p2,n+1=q2となる
①は思いつく人も多いのではないだろうか。しかし、①を思いついても答えが求められたことに安心して、②の可能性を見落とした受験生は多いと思う。
①の場合は言わずもがなn=2,n=-1であるが、②の場合はどうだろうか。差が3である二つの2乗の数を探してみると、n=3として、1と4が挙げられる(これ以降は差が大きくなっていくので、1と4以外はない)。
よってn=2,-1,3となる。
(9)
平面図形の問題。これも超典型的な補助線を引く問題(下図を参照)。
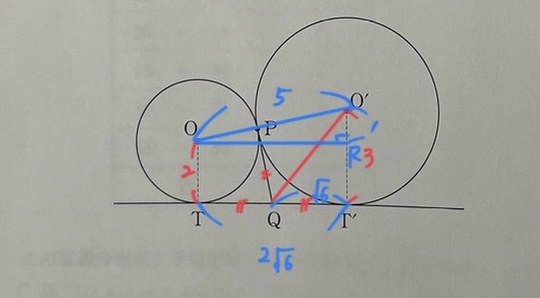
補助線により長方形と直角三角形に分け、三平方の定理を利用して答えを導く。
Ⅱ
(1)
三角比と平面図形の問題。問題にて30°と15°の角度が与えられているが、当然30°と15°の角度を利用した45°の角度についても注目する必要がある。
△ACDに注目して、正弦定理を使うとCDの長さが算出できる。
CEに関しては、中学3年生時の円の範囲が定着しているかどうかが重要。問題文で与えられた角度を円周角の定理で移動させると、角ACE=75°であることが分かる。
ということは、△ACEに注目すると、底角が等しいのでこれは二等辺三角形になる。
角CAE=30°、AC=AE=6であることが分かるので、余弦定理によりCEが求められる。
ちなみにここでも二重根号を外す必要があるので、計算問題を疎かにしていた受験生は悔しい思いをしたのではないだろうか。
(2)
(1)により、△ACEの三辺の長さは明らかになっているので、75°の角度を主人公とした余弦定理を作れば良い。
実はこの問題も合格を左右しうる問題である。なぜなら、正直に余弦定理を計算してしまうと、面倒な計算になってしまうからだ。
CEの長さの2乗とcos75°の係数は展開せずに計算すると、ちょうど最後に約分できるようになっている。
複雑な計算は最後まで展開しないのが鉄則である。
(3)
最後の問題については多様な解き方があるかと思うが、私はsinを使った三角形の面積公式で求めた。
△CDBのうち、角CBDは135°と求められ、CB、CDも長さが求められている。
残るはBDだが、△ACEと△DBEが相似であることを考えると、△DBEは二等辺三角形であるので、DB=DE=CD-CEと求められる。
看護医療系専門進学塾桜芽会の講習
2024年度春期講習の概要はこちら
オンライン
進学セミナー募集開始

無料LINE相談
随時受付中
無料
体験・相談
お申し込み


 アクセス
アクセス
