看護医療系専門進学塾の桜芽会です。

桜芽会では、各大学の看護系学科について、入試問題の解答解説を載せていきます。

今回は、2024年度 順天堂大学 医療看護学部 B日程（英語）の解答解説を載せます。

順天堂大学を志望している生徒は是非参考にしてください！

【講評】

大問は6問構成。簡単な問題と難しい問題の差が激しい。また、解法を知っていないと苦労する問題も散見される。

大問1は式変形と関数の問題。過剰なほど誘導がついているので、大問1は確実に得点しておきたい。この後に面倒な問題が控えていることを考えると、大問1、大問2あたりはサクサク進めていこう。

大問2はデータの問題。これも定義がわかっていれば難しい問題ではない。a取りうる範囲が少ないので、わからない場合はaに具体的な数を当てはめて試してみるのも良いだろう。

大問3は平面図形の問題。正弦定理、余弦定理を使う部分以外は、もしかすると中学数学の平面図形の能力がものを言うかもしれない。

円周角の定理をいかに上手く使えるかがポイント。

大問4は解の範囲が指定された二次方程式の問題。杏林大学の解答速報でも述べたが、教科書傍用問題集で言うと、B問題に入っているか、「研究」などの単元に収録されている。

後半は軸の場合分けが上手くできるかどうかがポイント。

大問5は確率の問題。これは解き方を知っている、知らないでかなり差が出た問題ではないだろうか。最後の問題はベン図が上手くイメージできたかどうかがポイント。

大問6は立体図形の問題。立体を切断して上手く平面図形の問題に帰着できたかどうかがポイント。内接球の半径の問題は、これも今年の杏林大学で出題されている。

平面図形の内接円の半径を面積から求める問題の解法が浮かんだ人は、問題なく解けた問題であるが、解法が分からなければ手も足も出なかっただろう。

【解答】

Ⅰ	解答	Ⅱ	解答	Ⅲ	解答	Ⅳ	解答	Ⅴ	解答	Ⅵ	解答
ア	5	ア	5	ア	1	ア	4	ア	1	ア	3
イ	1	イ	5	イ	8	イ	3	イ	2	イ	6
ウ	2	ウ	5	ウ	8	ウ	1	ウ	5	ウ	3
エ	4	エ	4	エ	1	エ	2	エ	2	エ	2
オ	7	オ	5	オ	6	オ	0	オ	1	オ	–
カ	5	カ	5	カ	7	カ	1	カ	6	カ	1
キ	–	キ	3	キ	7	キ	1	キ	6	キ	3
ク	2	ク	2	ク	2	ク	5	ク	1	ク	3
ケ	–	ケ	3	ケ	0	ケ	4	ケ	2	ケ	1
コ	5			コ	3			コ	1	コ	2
サ	2			サ	1			サ	6	サ	5
シ	–			シ	2			シ	1	シ	3
ス	5			ス	8			ス	9	ス	1
								セ	5	セ	8
								ソ	5	ソ	6
								タ	3	タ	3
								チ	2	チ	0
								ツ	4

【解説】

簡単な解説をしていきます。詳しい解説を知りたい方は、ぜひ桜芽会をご利用ください。

Ⅰ

（1）

（a）

対称式の問題。前半は普通にルートの計算を行い、後半は平方完成と通分で解く。

（b）

誘導が丁寧な四次関数の問題。tで置換すると二次関数の問題になるので、平方完成を行う。

Ⅱ

データ分析の問題。中央値は3番目と4番目の平均を取る。

この中央値を与えるaはについて、3番目と4番目のデータが変わらなければ良い。よって、a=0,1,2,3,4の5通り。

a=4以下のとき中央値は5.5、a=5のとき中央値は6、a=6のとき中央値は6.5、a=7以上の時中央値は7。よって4通り。

平均の公式について方程式を作ると、a=5が得られる。これを用いて分散と標準偏差を定義から求めると、それぞれ循環小数になるため、四捨五入を行う。

※通常√3などの値は問題で数値が与えられるはずだが、ご送付いただいた問題にはみられなかった。

Ⅲ

平面図形の問題。ア、イは△ABCにおいて余弦定理を用いて終了。

BDに関しては円周角の定理により、△BDCが二等辺三角形になることがわかれば、BD=DC=xとおいて、△BDCにおいて余弦定理を用いる。

その際、cosの値は円に内接する四角形の内角より、先ほど求めたcosBACからcosBDCを求めれば良い。

外接円の半径は△ABCにおいて正弦定理を用いれば終了。直径が導かれるので2で割るのを忘れずに。

△DBC、△ACDが二等辺三角形になることが分かったので、円周角の定理を用いて、△ABFが二等辺三角形であることを導くことでAFが求められる。

円周角の定理より、角BECと角BACが等しいので、△BCEにおいて余弦定理によりECの長さを求める。

すると、△BCEが二等辺三角形であることがわかる。これと円周角の定理を用いることにより、△ACEが二等辺三角形であることを導けばEAの値が求められる。

Ⅳ

前半は判別式の問題なのでさほど苦労はしないだろう。

中盤からは解の範囲が指定された二次方程式の問題。

軸、判別式、f(k)の正負、の3点に注目する（※）。

解の範囲が正負で分けられている場合は、kの値は0とすれば良い。

後半はやや面倒であるが、平方完成によって軸をmの式で表し、軸<1,1≦軸≦2,2<軸の3つの場合に分けて（※）を検討すれば良い。

Ⅴ

（a）

全部の場合は6の3乗で216。6の目が一度も出ない＝1〜5までの目で考えれば良い。

1〜5までの目の出方は5の3乗で125。

（b）

最も大きい数が5であることから、1〜5までの数の出方から、1〜4までの数の出方を引けば良い。

（c）

最も大きい目が5かつ、最も小さい目が1であることから、3回の試行のうち、2回は1と5が出ることになる。

目の出方の組み合わせを（1,◯,5）とすると、

（ⅰ）◯に1または5が入る時

（1,1,5）と(1,5,5)の並び方で6通り。

（ⅱ）◯に2〜4の数字が入るとき

3つの異なる数字の並び方で6通り。◯には2,3,4のどれかが入るので、3倍して18通り。

（d）

これは解法を知っていないと少し面倒な計算をすることになる。

まず、1〜5の目が出る場合を考える。しかしこれでは、1〜4の目が出た時（最大値が5にならない）、2〜5の目が出た時（最小値が1にならない）が数えられてしまうことになる。

そこで、この2つの場合を1〜5の目が出る場合から引くことを考えるが、これでは2〜4の目が出る場合が重複してしまう。（イメージは下図の通り）

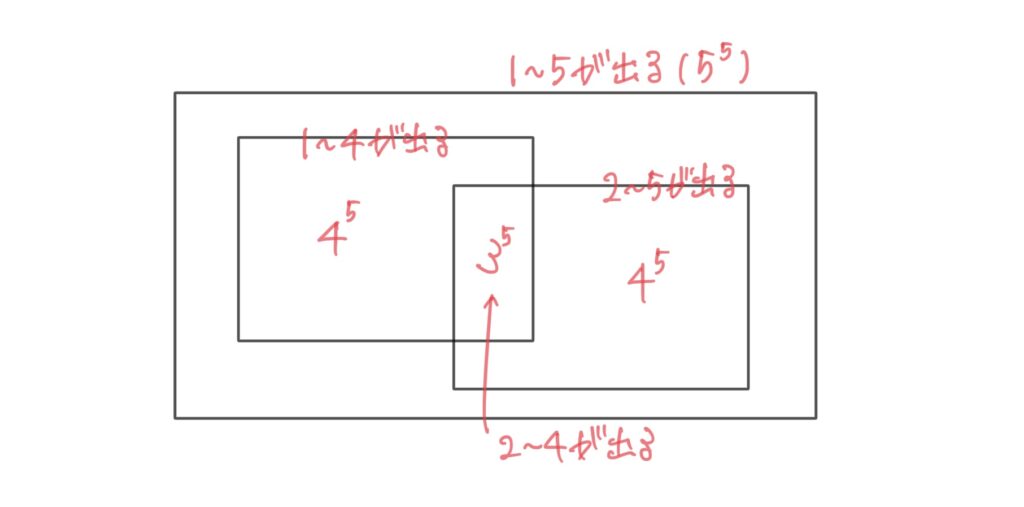
よって、1〜5の目が出る場合から、1〜4、2〜4の目が出る場合を引き、最後に重複している2〜4の目が出る場合を足して場合の数を求める。

Ⅵ

題意より、四面体ABEFの体積が四面体ABCDの9分の1になるので、底面積を比較することにより、BE:EC=BF:FD=1:2を導く。

BMはこの比と、△BCDのBからCDに下ろした垂線の長さから求めれば良い。

AからCDに下ろした垂線の足をHとし、A,B,Hを含む平面でこの四面体を切断することで、平面図形としてAMの長さを求める。

cosAMBについても、この平面上で△ABMにおいて余弦定理を用いれば良い。

△AEFの面積は、△AEFが二等辺三角形であることから、AM⊥EFなので、EFを相似によって求め、先ほどのAMと合わせて求めれば良い。

表面積は面積比計算によって求める。

最後の内接円の半径であるが、これは解き方を知らないと求めるのは難しいだろう。

平面図形の三角形の内接円の半径を、面積の方程式で求める方法の応用である。

内接する球の中心をO、半径をrとして、四面体ABEF=四面体OABF＋四面体OBEF＋四面体OAEF＋四面体OABEと考え、体積についての方程式を作る。

もともとの公式（体積をV、表面積をS、内接球の半径をrとしてV=1/3×r×S）を知っていれば瞬殺できる問題。

看護医療系専門進学塾桜芽会の講習

2024年度春期講習の概要はこちら

その他入塾やご質問事項に関しては、「お問い合わせ」または「LINE無料相談」からお気軽にご連絡ください。