看護医療系専門進学塾 桜芽会の看護医療系大学入試解答速報

桜芽会では、各大学の看護系学部について、入試問題の解答解説を載せていきます。

今回は、東京家政大学 健康科学部 2026年度 統一地区入試（1月23日実施） 数学の解答解説を載せます。

東京家政大学健康科学部を志望している生徒は是非参考にしてください！

※2026年入試のその他大学や科目の解答速報まとめは「【2026年看護医療系学部】 解答速報まとめ｜看護医療系専門進学塾 桜芽会」をご参照ください。

🌸桜芽会では毎年看護系大学/学部の入試解答速報を作っています🌸
問題用紙を返却された大学で、解答速報が欲しい！という方は、ご連絡ください。
X、Instagram、公式LINE、お問い合わせなんでも結構です。
看護医療系専門進学塾 桜芽会のSNS含む全メディアはこちら→https://lit.link/sakuragakai
なるべく解答速報を作ります！

※間違いを見つけた場合も上記からご連絡ください。確認し、訂正させていただきます。

2026年東京家政大学健康科学部統一地区（1月23日実施）数学 講評

一昨年と比較すると問題数が増加している（昨年は解答速報をやっていないので不明）。ということで、時間が足りなかったという受験者も多かったのではないだろうか。

特に大問1の小問集合で解くのに時間がかかってしまった、という人が多いと予想する。大問2以降は誘導も非常に丁寧で、特に時間を取られがちな図形問題でアプローチがすぐに確定する。よって、大問1の小問集合でペースを乱されずに、落ち着いて大問2以降でサクサク進めた人が有利だったと思われる。

驚くべきは一昨年と全く同じアプローチの図形問題が出題されていたことだ。
※参考「2024年度東京家政大学統一地区数学」(9)の問題。

これは過去問をしっかりと対策していた人にはラッキー問題だった。

2026年東京家政大学健康科学部統一地区（1月23日実施）数学 解答解説

I：小問集合

(1)絶対値方程式の問題。場合わけで解いても良いが、絶対値が一つかつ、変数がその絶対値の中に一つしかないので、定数だけを右辺に以降し、±で外すのが基本。

$$|1-2x|=5 \Rightarrow 1-2x=5\ \text{または}\ 1-2x=-5$$$$x=-2,\ 3$$

よって ③。

(2) 連立不等式の問題。連立不等式は左側と右側に分けて計算し、数直線を書いて範囲を求める。

左側：$$\frac{x}{4}+\frac13<\frac{4-x}{2} \Rightarrow 3x+4<24-6x \Rightarrow 9x<20 \Rightarrow x<\frac{20}{9}$$

右側：$$\frac{4-x}{2}\le \frac{2x-1}{3} \Rightarrow 12-3x\le 4x-2 \Rightarrow 14\le 7x \Rightarrow x\ge 2$$

合わせて$$2\le x<\frac{20}{9}$$

よって⓪。

(3) 三角形の問題。一瞬余弦定理が頭をよぎった受験生もいたかもしれないが、余弦定理だけでは解けない（辺の長さが一つ足りない）。本文は補助線を引いて、有名角を用いた辺の比を利用して解くか、角度が全て求められるので、正弦定理を利用して解く。本解説では前者を利用する。

$$\angle C=180^\circ-105^\circ-30^\circ=45^\circ$$

図のような補助線を引いて、比を用いて求める。

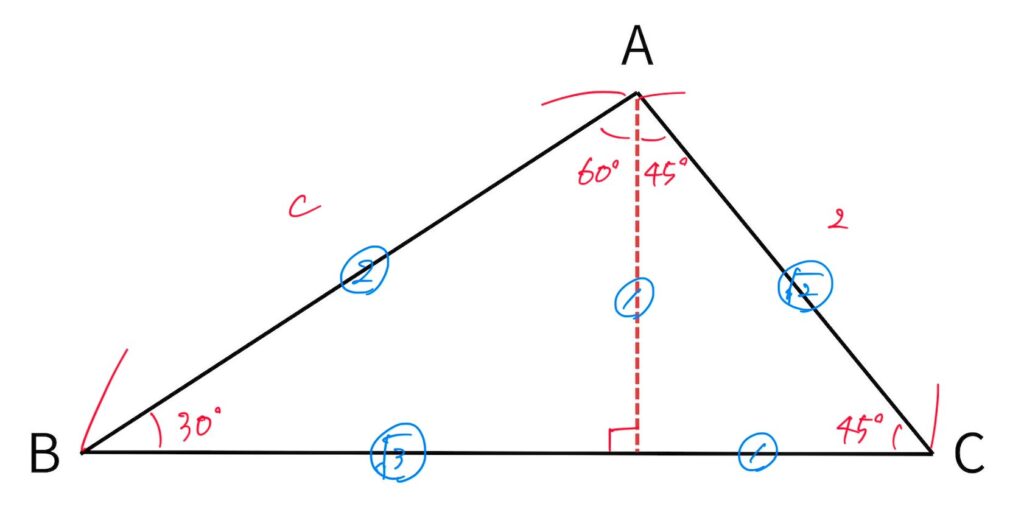
よって ③＝2，④＝2（$c=2\sqrt2$c=22​）。

(4) 四分位数（体重データ）の問題。データの数が多いので、四分位数の位置の計算を覚えていない人は、例えば9個のデータなど小さいデータを用意して、どこが求める四分位数になるかを具体的に試してみると良い。

データ数99のとき第3四分位数の位置：$$\frac{3(99+1)}{4}=75$$43(99+1)​=75

よって Q3は75番目。与えられた情報より75番目は64kgなので②（64）。

59kgを1つ追加して100個にすると位置：$$\frac{3(100+1)}{4}=75.75$$43(100+1)​=75.75

したがって 75番目と76番目の平均。
59kgは小さい側に入るので、元の74番目(63kg)→新75番目、元の75番目(64kg)→新76番目。$$Q_3’=\frac{63+64}{2}=63.5$$Q3′​=263+64​=63.5

よって ①（63.5）。

(5) まず変量が1回、2回、3回、4回であるということを確認する。1回目で2回同じ色が続くことはありえないので、変量が1の時の確率は0。ポイントは4回目の強制終了の際の確率である。

黒：B、白：Wとする。

① 2回目で終了する場合（N=2）

2回目で終了する＝1回目と2回目が同じ色。

起こりうる並び：BBまたはWW

確率：

• $P(BB)=\frac13\cdot\frac13=\frac19$
• $P(WW)=\frac23\cdot\frac23=\frac49$

したがって$$P(N=2)=\frac19+\frac49=\frac59$$② 3回目で終了する場合（N=3）

3回目で終了するには、

• 2回目では終了していない（＝1回目と2回目が違う）
• 3回目で「2回目と同じ」になって終了

つまり「1回目と2回目が違い、2回目と3回目が同じ」。

起こりうる並び：BWWまたはWBB

確率：

• $P(BWW)=\frac13\cdot\frac23\cdot\frac23=\frac{4}{27}$
• $P(WBB)=\frac23\cdot\frac13\cdot\frac13=\frac{2}{27}$

したがって$$P(N=3)=\frac{4}{27}+\frac{2}{27}=\frac{6}{27}=\frac29$$③ 4回目で終了する場合（N=4）

4回目まで行くには、2回目でも3回目でも終了していない必要があります。
つまり最初の3回が 交互になっていることが必要です。

最初の3回の並びは2通り：BWBまたはWBW

このあと4回目は

• 同色連続で終了（自然終了）してもよいし
• 同色連続がなくても強制終了

したがって起こりうる並びは次の4通り：BWBB（4回目でBBとなり自然終了）、BWBW（最後まで交互で強制終了）、WBWW（4回目でWWとなり自然終了）WBWB（最後まで交互で強制終了）

それぞれの確率：

• $P(BWBB)=\frac13\cdot\frac23\cdot\frac13\cdot\frac13=\frac{2}{81}$
• $P(BWBW)=\frac13\cdot\frac23\cdot\frac13\cdot\frac23=\frac{4}{81}$
• $P(WBWW)=\frac23\cdot\frac13\cdot\frac23\cdot\frac23=\frac{8}{81}$
• $P(WBWB)=\frac23\cdot\frac13\cdot\frac23\cdot\frac13=\frac{4}{81}$

合計：$$P(N=4)=\frac{2+4+8+4}{81}=\frac{18}{81}=\frac29$$

よって期待値は$$=2\cdot\frac59+3\cdot\frac29+4\cdot\frac29 =\frac{10+6+8}{9}=\frac{24}{9}=\frac83$$

(6) 放物線の平行移動の公式と、対称移動の公式が頭に入っているかどうか。

まず平行移動：左に1、上に1なので$$y=f(x+1)+1$$$$=-(x+1)^2+4(x+1)+1=-x^2+2x+4$$

次に $x$軸対称（符号反転）：$$y= -(-x^2+2x+4)=x^2-2x-4$$

よって ⑨＝2，⑩＝4。

(7) 連立不等式の問題。面倒くさがらずに数直線を書いて、最終的な範囲を求めること。本文は二つとも因数分解が可能なので、ミスの内容確実に得点したい。④（選択肢④）。

(8) 高校受験経験者に有利な問題。下図のような補助線を引いて長方形を作ることと、円外の1点から引いた接点までの線分の長さが等しいことを思い出すことができれば、三平方の定理と長方形の性質を利用して解くことができる。

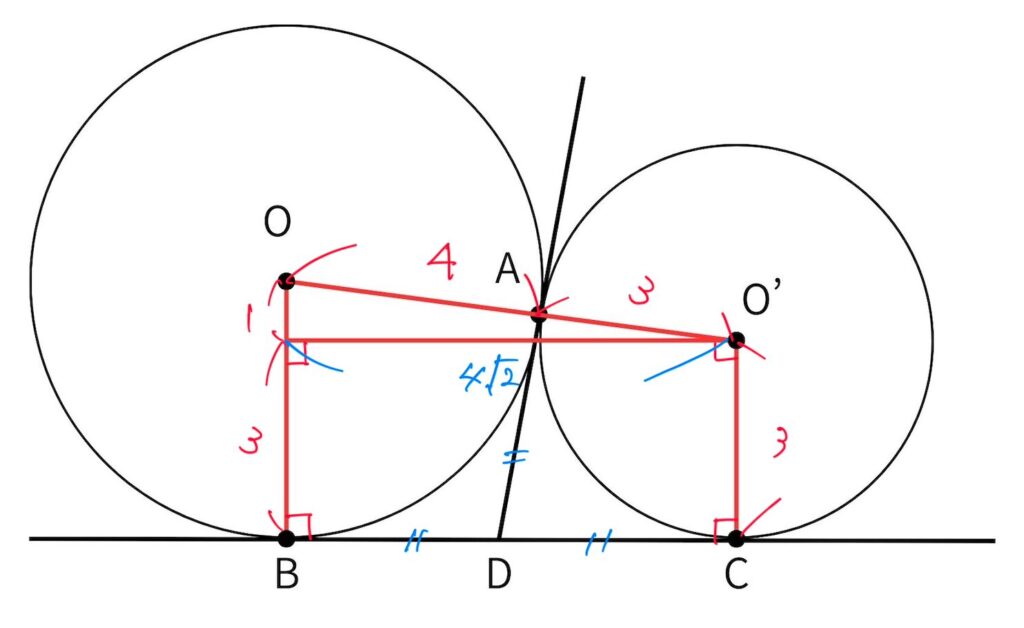
よって ⑫＝2，⑬＝3。

(9) これは確実に得点しておきたい問題。否定すると「かつ」が「または」に変わることに注意。$$x\le 0\ \text{または}\ x=1$$

よって ③（選択肢③）。

II：平面図形

(1) 方べきの定理を覚えていれば得点できる問題。誘導が親切。$$PB\cdot PA=PC\cdot PD$$

$$3\cdot 4=PC(PC+4) \Rightarrow PC^2+4PC-12=0 \Rightarrow PC=2$$※「辺の長さ」なので負の解は不適

よって ⑮＝2。

(2) この問題もメネラウスの定理を覚えていれば得点できる。誘導が親切。$$\frac{AB}{BP}\cdot \frac{PD}{DC}\cdot \frac{CQ}{QA}=1$$

よって ⑯＝1，⑰＝2。

(3)(2)と同様。$$\frac{BA}{AP}\cdot \frac{PC}{CD}\cdot \frac{DQ}{QB}=1$$

よって ⑱＝1，⑲＝8。

(4) 方べきの定理からa:b=2:1であることを求め、c,dの比を調整する。

$$QA\cdot QC=QB\cdot QD \Rightarrow ac=bd$$

(2)(3)より
$$a\cdot 2a=b\cdot 8b \Rightarrow 2a^2=8b^2 \Rightarrow a=2b$$

よって$$a:b:c:d=2:1:4:8$$

よって ⑳＝2，㉑＝1，㉒＝4，㉓＝8。

(5) ここまでの問題が解けていれば、△APDの面積を基準にして面積の比を求めることができる。

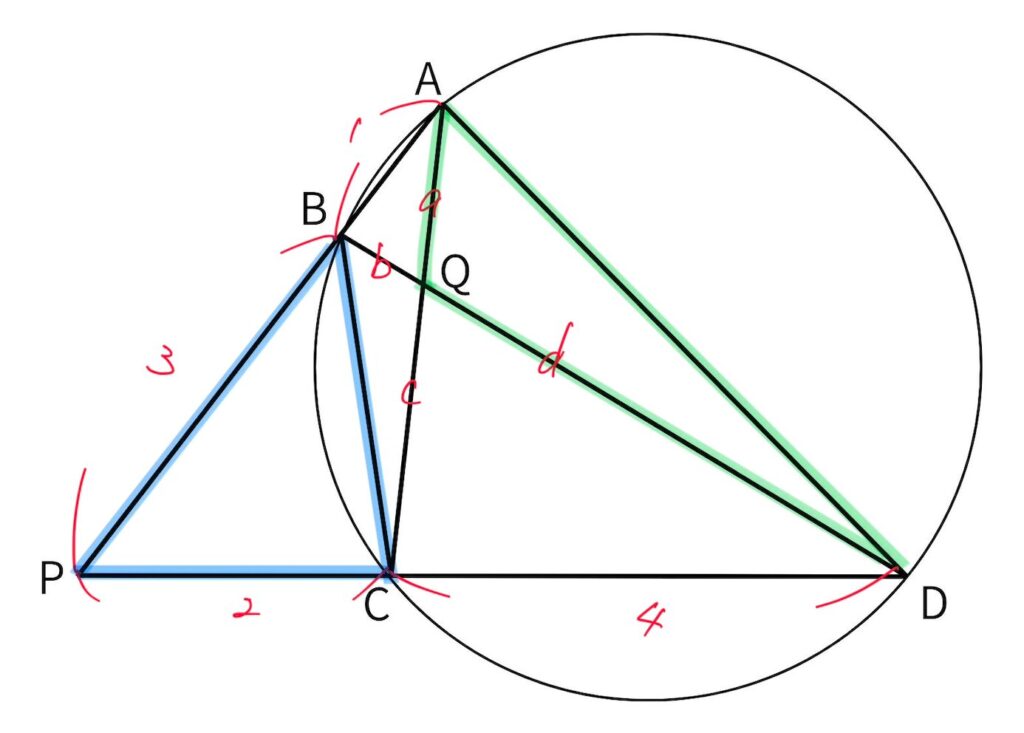
よって ㉔＝9，㉕＝8。

III：確率

(1)計算で求めても良いが、計算に自身のない人は数え上げても問題ない。

• 絵札：$\frac{12}{52}=\frac{3}{13}$
  ㉖＝3，㉗＝1，㉘＝3
• ハート：$\frac{13}{52}=\frac{1}{4}$
  ㉙＝1，㉚＝4
• 絵札またはハート：$\frac{22}{52}=\frac{11}{26}$
  ㉛＝1，㉜＝1，㉝＝2，㉞＝6

(2) 一枚引いたカードを元に戻してもう一度引くので、独立試行である。「少なくとも」ときたら余事象を使うという典型パターン。

$$p=\frac{11}{26} \Rightarrow 1-(1-p)^2 =1-\left(\frac{15}{26}\right)^2 =1-\frac{225}{676} =\frac{451}{676}$$

よって ㉟＝4，㊱＝5，㊲＝1，㊳＝6，㊴＝7，㊵＝6。

(3) (2)と同じパターンだが、こちらは一度引いたカードを戻さないので、非独立試行。余事象をつ買うことは同じ。

2回とも「絵札でもハートでもない」を全体から引く：$$1-\frac{30}{52}\cdot\frac{29}{51} =1-\frac{435}{1326} =\frac{891}{1326} =\frac{297}{442}$$

よって ㊶＝2，㊷＝9，㊸＝7，㊹＝4，㊺＝4，㊻＝2。

IV：背理法による証明

正直この問題には面食らった人も多いのではないだろうか。看護系入試の数学＝穴埋めだから証明は出ない、という割り切った考え方で勉強していると少し難しく感じたかもしれない。とはいえ、誘導は丁寧なので、落ち着いて問題文をよく読めば、背理法を忘れていても手をつけられる問題である。

(1) $\sqrt{12}=\frac{a}{b}$12​=ba​ とおくときの条件。これは背理法のやり方を覚えていないと厳しかったかもしれない。背理法で矛盾を出すには 既約分数で置く必要があることを思い出そう。よって「a,bは自然数で、1以外の正の公約数をもたない」

選択肢②。

(2) 「$a^2$a2が12の倍数ならaは12の倍数」の反例の最小a

$a^2$が12の倍数でもaが12の倍数とは限らない。最小となるaは調べていけばすぐに求められる。
(1)が解けなかったとしてもこれは調べるだけなので得点しておきたい。

㊽＝6。

(3) この問題も落ち着いて文章をよく読めば、答えが導けるはずだ。2乗して12の倍数にならなければならないので、

$a^2$が4の倍数→aは2の倍数、
$a^2$が3の倍数→aは3の倍数。
よって aは2の倍数かつ3の倍数（選択肢⓪）。
㊾＝⓪。

(4) 対偶の取り方を覚えていれば瞬殺問題。

対偶は「aが3の倍数でないなら、$a^2$は3の倍数でない」＝選択肢②。

(5) 本文では2乗数がある数（例えば3）の倍数であれば、元の数もその数の倍数であることが問題文で述べられている。各選択肢を落ち着いて吟味すれば、得点できる問題である。

• ③「$6b^2$が9の倍数ならbは9の倍数」は偽（b=3で反例）。
  よって 選択肢③
  

(6) 背理法で既約分数を仮定しているので、途中で aもbも3の倍数が出れば「公約数3をもつ」ので矛盾。よって選択肢④。

看護医療系専門進学塾桜芽会へのお問い合わせ

その他入塾やご質問事項に関しては、「お問い合わせ」または「LINE無料相談」からお気軽にご連絡ください。