
看護医療系専門進学塾 桜芽会の看護医療系大学入試解答速報
桜芽会では、各大学の看護系学部について、入試問題の解答解説を載せていきます。
今回は、東京家政大学 健康科学部 2026年度 統一地区入試(1月24日実施) 数学の解答解説を載せます。
東京家政大学健康科学部を志望している生徒は是非参考にしてください!
※2026年入試のその他大学や科目の解答速報まとめは「【2026年看護医療系学部】 解答速報まとめ|看護医療系専門進学塾 桜芽会」をご参照ください。
🌸桜芽会では毎年看護系大学/学部の入試解答速報を作っています🌸
問題用紙を返却された大学で、解答速報が欲しい!という方は、ご連絡ください。
X、Instagram、公式LINE、お問い合わせなんでも結構です。
看護医療系専門進学塾 桜芽会のSNS含む全メディアはこちら→https://lit.link/sakuragakai
なるべく解答速報を作ります!
※間違いを見つけた場合も上記からご連絡ください。確認し、訂正させていただきます。
2026年東京家政大学健康科学部統一地区(1月24日実施)数学 講評
大問1は24日実施の数学と比べると若干時間がかからないかもしれないが、それでも計算やアプローチで引っかかると時間をロスしてしまう。
23日実施の数学同様、いかに大問2以降の問題で時間を節約できたかどうかがカギとなる。特に大問2に関しては、誘導が非常に丁寧なので、アプローチに迷うことはなかったのではないだろうか。ここはサクサクと解いていきたい。
大問3は軸が動くパターンの二次関数の最大最小問題で、これも学校の問題集に必ず収録されている問題。アプローチには迷わなかったはずだ。ただ、面倒くさいのでいかに早く正確に解くことができるかが重要。
大問4に関しても、体積を2通りで表して高さを求める有名問題。23日の数学では背理法が出題され、面食らった受験生もいるかと思うが、それに比べると、誘導があるので解法を知らない受験生もある程度戦える問題である。
2026年東京家政大学健康科学部統一地区(1月24日実施)数学 解答解説
Ⅰ
(1)3乗の展開公式が頭に入っていれば解ける。確実に得点すべき問題。
①=8,②=3,③=6,④=5,⑤=4,⑥=2,⑦=7
(2)有理化の問題。こちらも有理化の公式が頭に入っていれば解ける。確実に得点すべき問題。
⑧=5,⑨=6,⑩=6,⑪=6
(3) 1週間ではなく、6日というところに気を付ける。平均と分散の公式が頭に入ってれば解ける。
平均
分散(母分散)
⑫=7,⑬=3,⑭=2,⑮=6,⑯=9
(4) 集合の問題。4の倍数と6の倍数を引いた後に、重複して引いた12の倍数を足しても良いし、下記のように考えても良い。
4の倍数は25枚除去。次に6の倍数を「残りから」除去 ⇒ 6の倍数16枚のうち12の倍数8枚は既に除去済みなので追加で8枚除去。
⑰=6,⑱=7
(5) 命題の問題。こちらも逆・裏・対偶の関係性がわかっていれば難なく正解できる。
,
(i) 逆・裏・対偶(選択)
- 逆 :②
- 裏 :①
- 対偶 :③
⑲=2,⑳=1,㉑=3
(ii) 真偽(0=真, 1=偽)
まず範囲:
よって
- 元の命題:でも で となり 偽
- 逆: なので 真
- 裏: または なので 真
- 対偶:元と同値なので 偽
㉒=1,㉓=0,㉔=0,㉕=1
(6) 立体図形の問題。図が少しややこしいので、最初にどの面で考えるかがすぐに分かるかが勝負。
△ABD は直角三角形で ∠B=30∘ なので
△ABCで正弦定理を用いて を出す。
㉖=1,㉗=5,㉘=2
(7) 二次方程式と判別式の問題。誘導はないが、「常に成立」ときたら、二次関数のグラフの形を考えたことを思い出そう。
判別式
- 常に >0(下に凸なので全域正ならば)⇒ (浮いてるようなグラフ)
選択肢 ②
㉙=2
- 不等式 <0 が解をもつ(どこかで負になる)⇒
選択肢 0
㉚=0
(8) 与えられた3点から二次関数の式を決定する問題。通常の一般式に代入して三元一次連立方程式を解いても良いが、よく見ると与えられた3点のうち2点はx軸との交点を表しているので、下記の一般式を用いると時間が節約できる。
x=31 を代入すると
㉛=−,㉜=3,㉝=2,㉞=8,㉟=3
(9) 三角形の成立条件を覚えているかどうか。すべての辺について「2辺の和は他の1辺より長い」という関係が成り立つ。
選択肢 ④
㊱=4
Ⅱ 二等辺三角形と5心に関する問題
(1) 3:4:5の三角形になっていることが見抜ければ、計算なしでも一瞬で答えが出る。
重心Gは中線を に内分するので
㊲=4,㊳=8,㊴=3
(2) 外接円半径 を求める問題だが、流石に誘導が過剰すぎる。
図より は 上、
直角△OBMで三平方の定理より
㊵=2,㊶=5,㊷=8
(3) 内接円半径 とくれば解法は一瞬で思い浮かぶはず。この解法は看護入試では必須。必ず押さえておかなければならない解法。三角形を3つの三角形に分けて、面積で方程式を作る。
面積 、半周長
内心IはAM上で、BCからの距離が なので
㊸=3,㊹=2,㊺=5,㊻=2
(4)垂心の問題は少し珍しいが、難問奇問ではないので落ち着いて対応しよう。AF=xとでもおいて他の辺をxを用いて表し、△ACFと△BCFにおいて三平方の定理を利用し、FCの長さを2通りで表して方程式を作れば良い。
AHは△AFHと△AMBの相似を利用して求める。
㊼=7,㊽=5,㊾=7,㊿=4
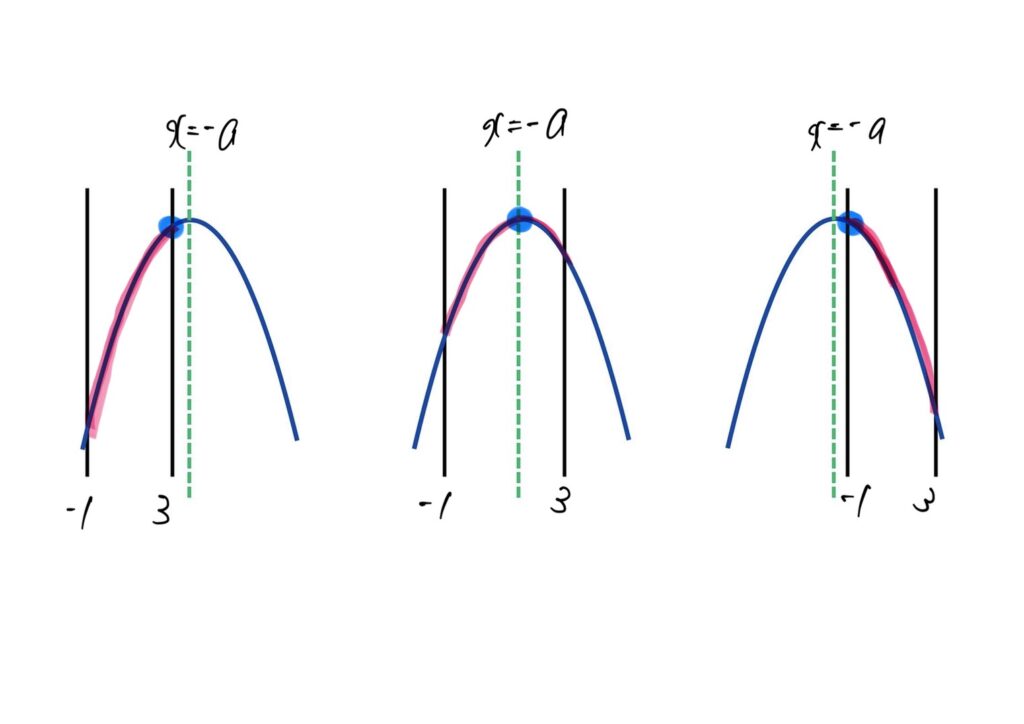
Ⅲ 二次関数の最大最小(軸が動くパターン)
軸は (上に凸の放物線なので最大は頂点側)。
(1) 最大値

- (頂点が右)⇒最大は のとき
→選択肢②
- (頂点が区間内)⇒最大は のとき
→選択肢③
- (頂点が左)⇒最大は のとき
→選択肢0
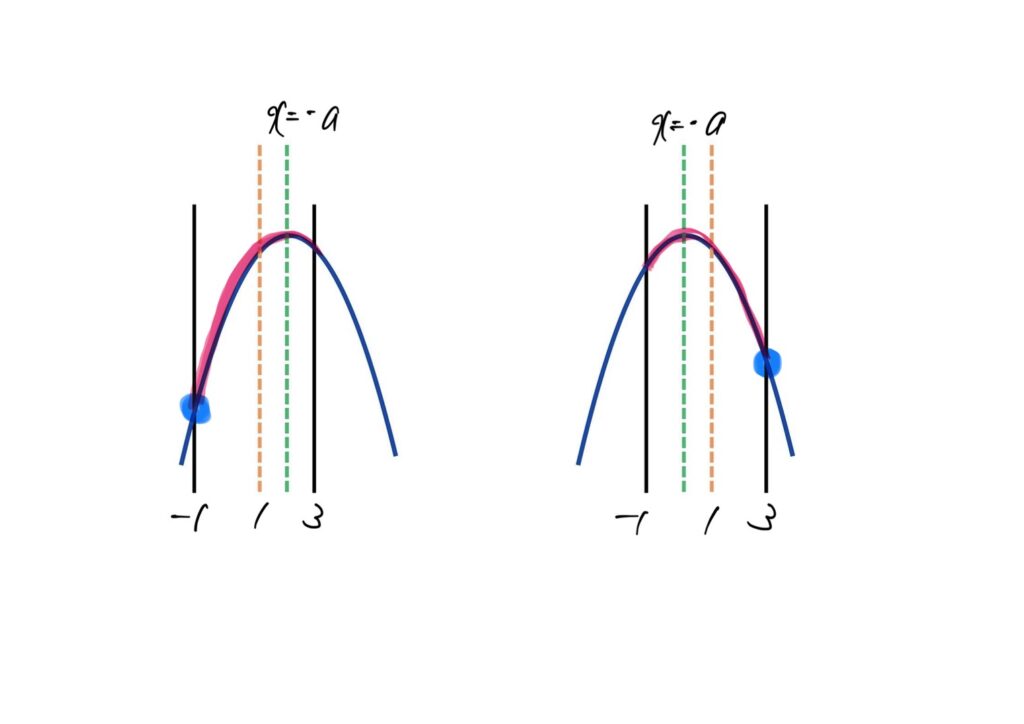
(2) 最小値

- :最小は のとき ⇒ (選択肢0)
- :最小は のとき⇒ (選択肢②)
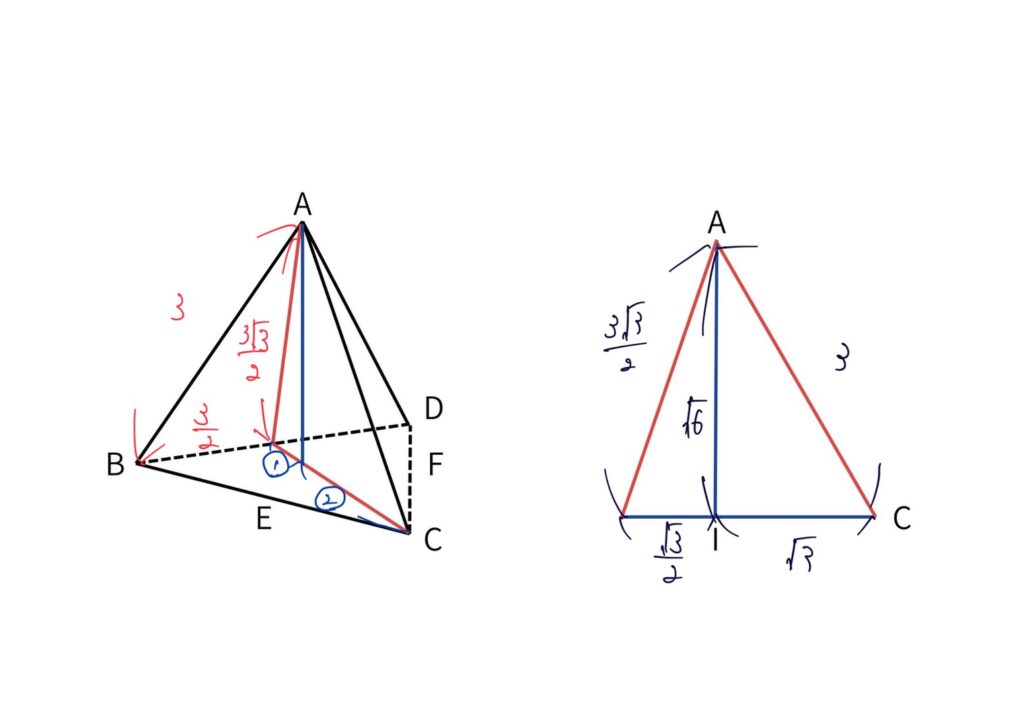
Ⅳ 四面体
(1)余弦定理を使う問題だが、これも誘導が過剰気味。余弦定理を使う三角形まで教えてくれているので、時間をかけずに解きたい。
△ABEで
同様に △ACF でも
よって7
△AEFで
よって5、7
(2) △AEFの面積 を求めるために、cosθからsinθを算出する。
三角形の面積公式を用いて
よって6
(4)この問題は切り口の平面がイメージできたかどうかが重要。切り口自体はオーソドックスかつ誘導されているので、問題なかったはず。

底面を△CEF(平面BCD上)とすると、高さは正四面体の高さ
△CEFは 、なす角60°
よって2
(4)体積を2通りの方法で表せるので、問題文の誘導にしたがって方程式を作り、CHを求める。
よって3
看護医療系専門進学塾桜芽会へのお問い合わせ
その他入塾やご質問事項に関しては、「お問い合わせ」または「LINE無料相談」からお気軽にご連絡ください。




 アクセス
アクセス
